Triangulation nodes help convert geometry into triangle-based mesh structures for processing and export. All the nodes are explained below.

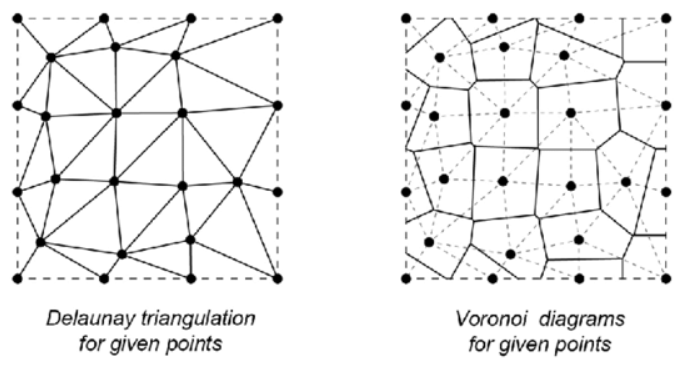
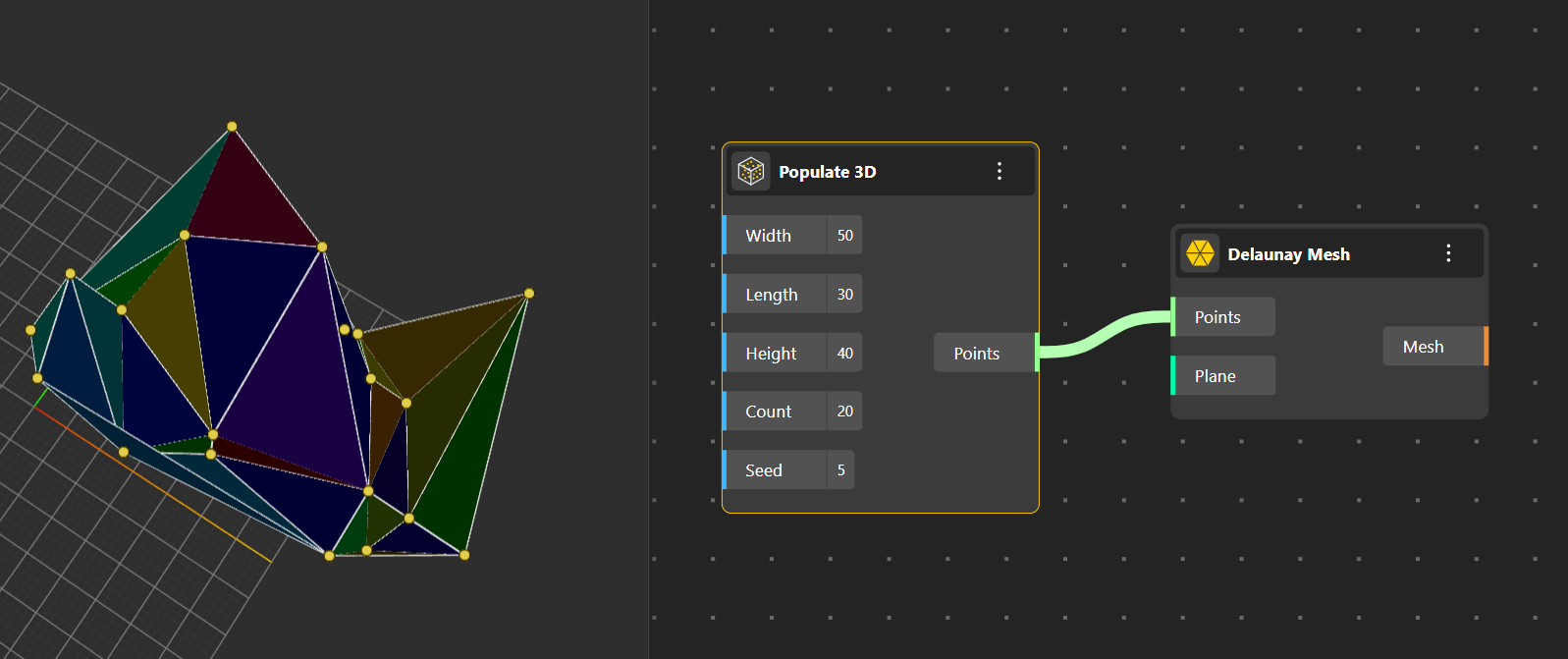
Delaunay triangulation is a way to connect a set of points with triangles so that the mesh looks as “regular” as possible. The rule is that no point should lie inside the circle that passes through the three corners of any triangle. This method avoids skinny, stretched triangles and produces a network of well-shaped, stable triangles that are useful in modeling surfaces, simulations, and terrain mapping. Think of it as connecting dots in a way that makes the triangles as balanced and neat as possible.
A Voronoi diagram divides space into regions based on a set of points. Each region contains all the locations that are closer to its point than to any other point. Imagine dropping seeds on a flat field, and then each seed claims the area around it that is nearest to it, those are the Voronoi cells. This concept is widely used in fields like urban planning, biology, computer graphics, and pathfinding because it naturally shows zones of influence or proximity.
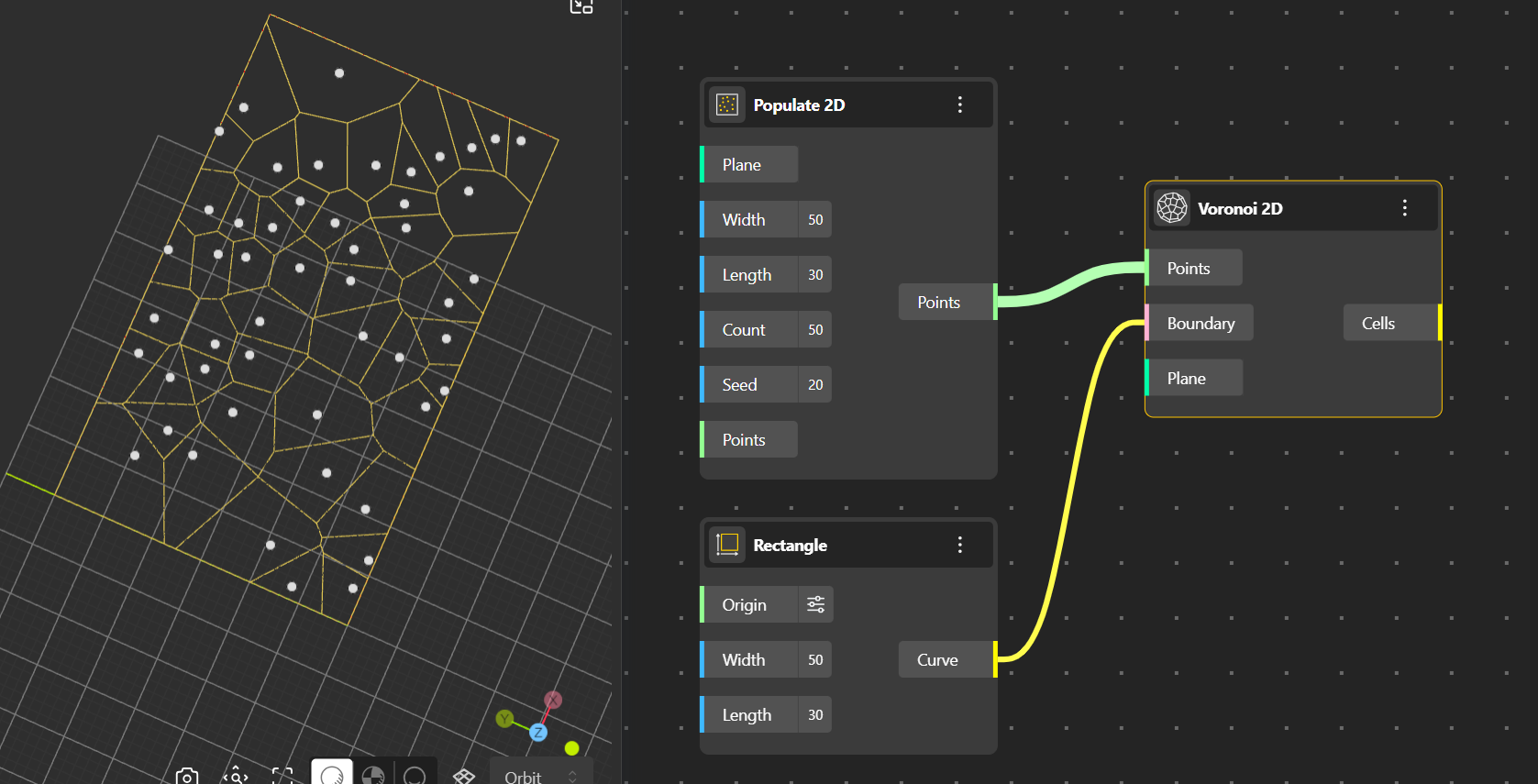
Voronoi 2D: Generates a 2D Voronoi diagram from a set of input points. The plane is divided into regions where each region contains all locations closest to one specific point.
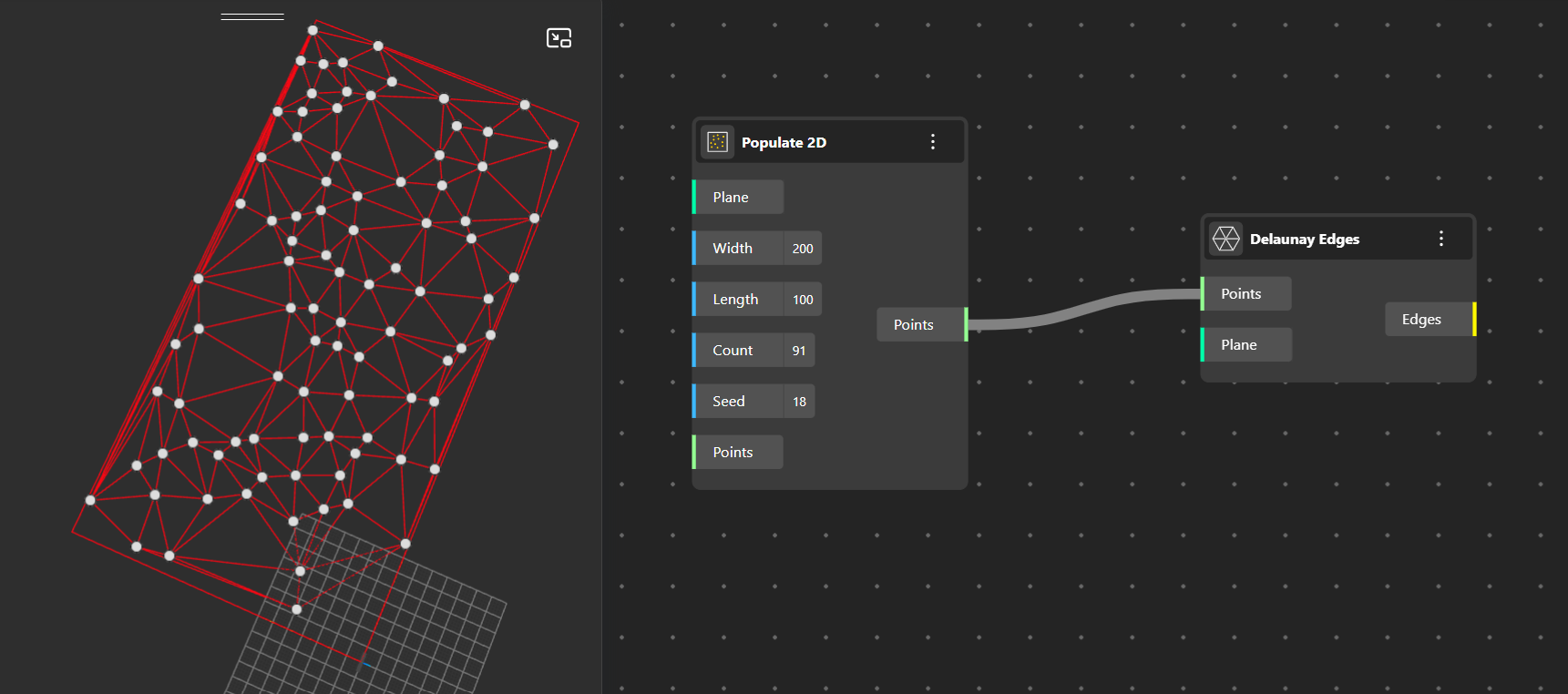
Delaunay Edges: Produces the line connections between points that form the Delaunay triangulation. These edges represent the dual structure of the Voronoi diagram and show how points are connected without overlapping triangles.
Delaunay Mesh: Creates a full triangle mesh from the Delaunay triangulation. This output includes triangular faces that fill the space between connected points, useful for meshing, simulation, and surface generation.
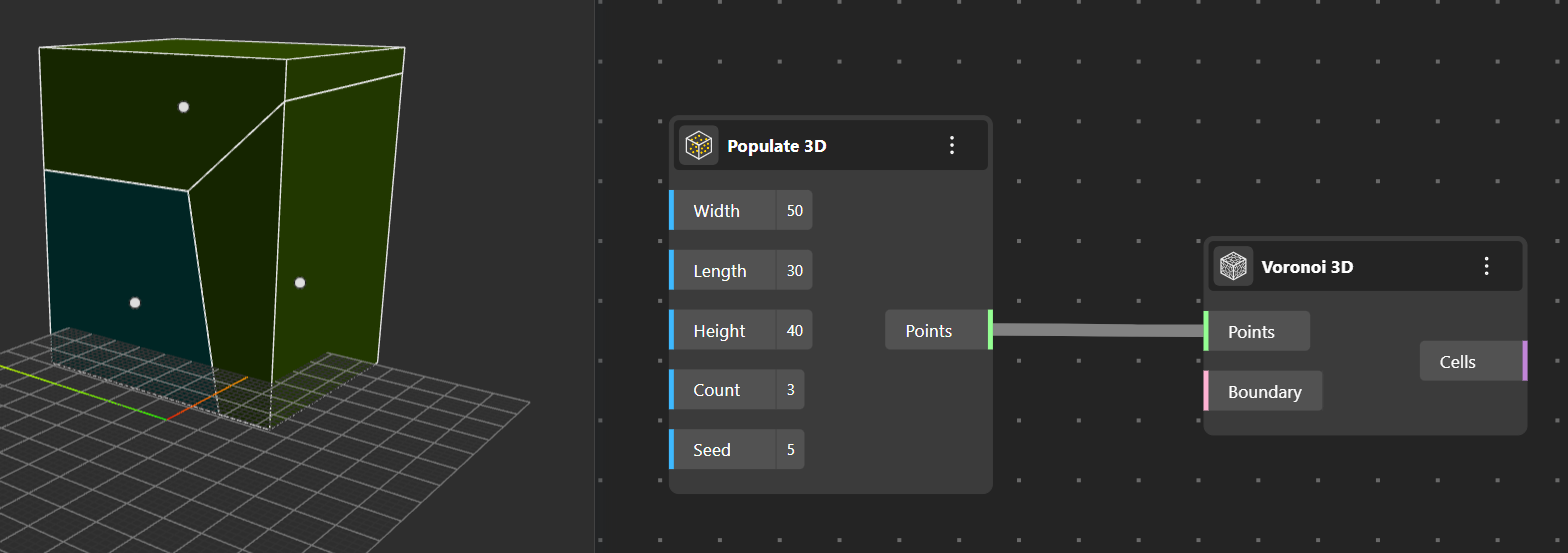
Voronoi 3D: Generates a 3D Voronoi diagram from input points. Instead of flat 2D cells, it builds volumetric polyhedral cells where each volume contains all points in space closest to one input point.